Another Way of Conceptualising Division:

(Click the below link for a Microsoft Word version of this blog-post)

another_way_of_conceptualising_division

(Click the below link for a pdf version of this blog-post)

another_way_of_conceptualising_division

 

Figure 1:  The Division operator.  I drew this with pens, pencils, rulers and compass.

Introduction:

What follows is a discussion of Quotative Division.

Body:

 

We want an implicit understanding of the operation of Division.

Let us take the equation:

8  ÷  4 = 2

and let us examine what is happening, conceptually, when this operation is being worked out.  Let us imagine our dividend:

8

as a Universal Set containing 8 elements:

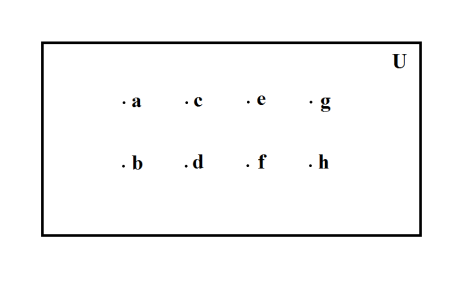
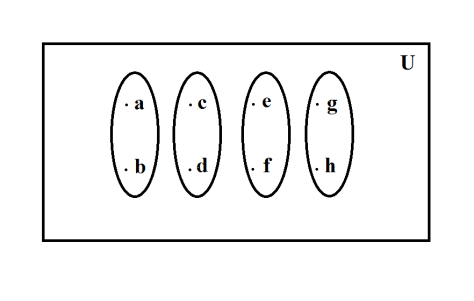
Figure 2:  A Universal Set containing the dividend number of elements.  A Universal Set containing 8 elements.  The set {a,b,c,d,e,f,g,h} .

I have 8 elements, the dividend, and I want a quotient number of sets that will contain 4 elements, the divisor, apiece. How many sets do I need?

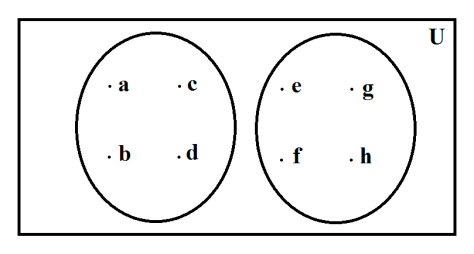
Figure 3:  We have a dividend quantity of elements, and we wish to disperse this dividend quantity of elements, evenly, such that we arrive at a divisor quantity of elements in each set.  The quantity of sets that it takes to do this is the quotient.  In the above-depicted example, we have 8, the dividend, elements; we wish to disperse these 8 elements, evenly, such that we obtain 4, the divisor, elements in each set.  The number of sets that it takes to achieve this even dispersal, i.e. 2, is the quotient.

The number of sets that I need to disperse 8, the dividend, number of elements, evenly, such that I obtain 4, the divisor, elements in each set is:

2

Therefore:

2

is the quotient.  If we were doing “Sums” in primary school, then:

2

would be “the answer.”

We take the set:

{a,b,c,d,e,f,g,h}

and we disperse these 8, the dividend, elements, such that each set contains 4, the divisor, elements:

{a,b,c,d} {e,f,g,h}

We are left with 2, the quotient, number of sets.

One Way of Conceptualising Division:

(Click the below link for a Microsoft Word version of this blog-post)

one_way_of_conceptualising_division

(Click the below link for a pdf version of this blog-post)

one_way_of_conceptualising_division

Figure 1:  The Division Operator.

Introduction:

What follows is a discussion of Partitive Division.

Body:

 

We want an implicit understanding of the operation of Division.

Let us take the equation:

8  ÷  4 = 2

and let us examine what is happening, conceptually, when this operation is being worked out.  Let us imagine our dividend:

8

as a Universal Set containing 8 elements:

Figure 2: A Universal Set containing the Dividend number of elements.  A Universal Set containing 8 elements.  The set {a,b,c,d,e,f,g,h} .

Let us say that we wished to divide these elements, evenly, amongst a divisor number of sets.  The divisor is:

4

in this instance.  So we wish to distribute 8 elements, evenly, amongst 4 sets:

Figure 3:  We have distributed a dividend number of elements, evenly, amongst a divisor number of sets.  The number of elements in each set is the quotient.  We have distributed 8 elements, evenly, amongst 4 sets.  2, the number of elements in each set, is the quotient.

If we distribute 8 elements, evenly, amongst 4 sets, then we obtain 2 elements in each set.  2 is the result of Division.  If we were doing “sums” in primary school, then 2 would be “the answer.”

We have taken 1 big set containing 8 elements:

{a,b,c,d,e,f,g,h}

and we have dispersed these elements evenly amongst 4 sets:

{a,b} {c,d} {e,f} {g,h}

The number of elements in each of these 4 sets, i.e.:

2

is the quotient.