When it comes to the Kindle Store: prospective purchasers really do judge a book by its cover!
That is why a book cover requires its being extremely stylish and appealing to the eye, employing gradients, fonts, contrasting/complementary colours, etc. to this effect.
(Click the below link for a Microsoft Word version of this blog-post)
another_way_of_conceptualising_division
(Click the below link for a pdf version of this blog-post)
another_way_of_conceptualising_division
Figure 1: The Division operator. I drew this with pens, pencils, rulers and compass.
What follows is a discussion of Quotative Division.
We want an implicit understanding of the operation of Division.
Let us take the equation:
8 ÷ 4 = 2
and let us examine what is happening, conceptually, when this operation is being worked out. Let us imagine our dividend:
8
as a Universal Set containing 8 elements:
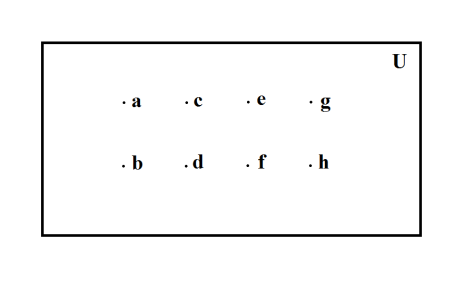
Figure 2: A Universal Set containing the dividend number of elements. A Universal Set containing 8 elements. The set {a,b,c,d,e,f,g,h} .
I have 8 elements, the dividend, and I want a quotient number of sets that will contain 4 elements, the divisor, apiece. How many sets do I need?
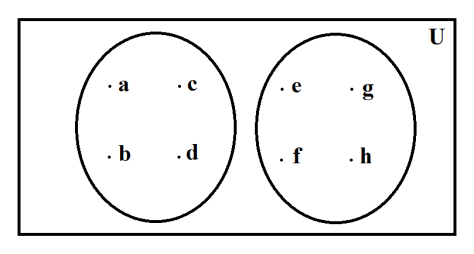
Figure 3: We have a dividend quantity of elements, and we wish to disperse this dividend quantity of elements, evenly, such that we arrive at a divisor quantity of elements in each set. The quantity of sets that it takes to do this is the quotient. In the above-depicted example, we have 8, the dividend, elements; we wish to disperse these 8 elements, evenly, such that we obtain 4, the divisor, elements in each set. The number of sets that it takes to achieve this even dispersal, i.e. 2, is the quotient.
The number of sets that I need to disperse 8, the dividend, number of elements, evenly, such that I obtain 4, the divisor, elements in each set is:
2
Therefore:
2
is the quotient. If we were doing “Sums” in primary school, then:
2
would be “the answer.”
We take the set:
{a,b,c,d,e,f,g,h}
and we disperse these 8, the dividend, elements, such that each set contains 4, the divisor, elements:
{a,b,c,d} {e,f,g,h}
We are left with 2, the quotient, number of sets.
Figure 1: The JavaScript Logo. I drew this with pencils.
Figure 2: The schematic symbol for an And Gate.
The logical permutations of an And Gate are as follows:
0 ∧ 0 = 0
0 ∧ 1 = 0
1 ∧ 0 = 0
1 ∧ 1 = 0
The above can be read, in English, as follows:
Zero conjunction zero equals zero.
Zero conjunction one equals zero.
One conjunction zero equals zero.
One conjunction one equals one.
Alternatively:
Zero AND zero equals zero.
Zero AND one equals zero.
One AND zero equals zero.
One AND one equals one.
We can realise the above Boolean Logic in Digital circuitry, as follows:
Figure 3: An AND Gate. Notice how, this time, the switches, x and y are in series. In the Inclusive-Or gate, the switches, x and y were in parallel. The above-depicted And Gate represents the Boolean Equation, 0 ∧ 0 = 0
Figure 4: This And gate represents the Boolean Equation, 0 ∧ 1 = 0
Figure 5: This And gate represents the Boolean Equation, 1 ∧ 0 = 0
Figure 6: This And gate represents the Boolean Equation, 1 ∧ 1= 1
It is possible to translate Boolean Equations into Conventional-Arithmetic Equations, and to obtain the same logical result:
x ∧ y = x ( y)
Because:
x conjunction y
in Boolean Arithmetic equates to:
x multiplied by y
in conventional arithmetic, the logical output of an And Gate is termed:
the logical product
.
0 ∧ 0 = 0 (0) = 0
0 ∧ 1 = 0 (1) = 0
1 ∧ 0 = 1 (0) = 0
1 ∧ 1 = 1(1) = 1
It is possible to use the above logical translations so as to create buttons in JavaScript that calculate the logical permutations of an And gate.
Figure 7: The HTML-5 file that we need to program a web-app that calculates the truth-table of an And gate.
Figure 8: In the above-depicted JavaScript file, we declare four functions. Each function describes a logical permutation of the And Gate.
In the web-app that we have just programmed, we have created 4 buttons. Each button calculates a logical permutation of the And gate and displays the result in a dialog box.
Figure 9: A Screenshot of the web-app that we have just programmed in JavaScript.
You can test the above-described web-app for yourself by clicking on the following link:
Maths and Comedy 